About
Life
Daily Notes

3070. Count Submatrices with Top-Left Element and Sum Less Than k

4 min read

SOLUTION:

class Solution {
public:
  int countSubmatrices(vector<vector<int>>& grid, int k) {
      int n = grid.size();
      int m = grid[0].size();
      int ans = 0;
      vector<vector<int>> dp(n, vector<int>(m,0));
      for(int i=0;i<n;i++){
          for(int j=0;j<m;j++){
              if(i==0 && j==0){
                  dp[i][j]= grid[i][j];
              }
              else if(i==0){
                  dp[i][j] = dp[i][j-1] + grid[i][j];
              }
              else if(j==0){
                  dp[i][j] = dp[i-1][j] + grid[i][j];
              } else {
                      dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + grid[i][j];
              }
 
              if(dp[i][j]<=k) ans++;
          }
      }
      return ans;
  }
};

EASIER ALTERNATIVE SOLUTION:

class Solution {
public:
    int countSubmatrices(vector<vector<int>>& grid, int k) {
        int n = grid.size();
        int m = grid[0].size();
        int ans = 0;
        vector<vector<int>> dp (n+1, vector<int>(m+1,0));
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + grid[i-1][j-1];
                if(dp[i][j]<=k) ans++;
            }
        }
        return ans;
    }
};

Problem Understanding

Key Constraint: All valid submatrices must contain the top-left element (grid[0][0]) of the original matrix.

This means every valid submatrix has:

  • Top-left corner at (0, 0)

  • Bottom-right corner at some position (i, j)

Core Insight

Since all valid submatrices start from (0,0), we need to:

  1. Find all possible bottom-right corners (i, j)

  2. For each (i, j), calculate sum from (0,0) to (i,j)

  3. Count how many of these sums are ≤ k

DP Array Construction - Thought Process

Why 2D Prefix Sum?

  • Goal: Calculate sum from (0,0) to any (i,j) efficiently

  • Naive approach: For each (i,j), iterate through all cells from (0,0) to (i,j) → O(n²m²) time

  • Smart approach: Build incrementally using previously computed sums → O(nm) time

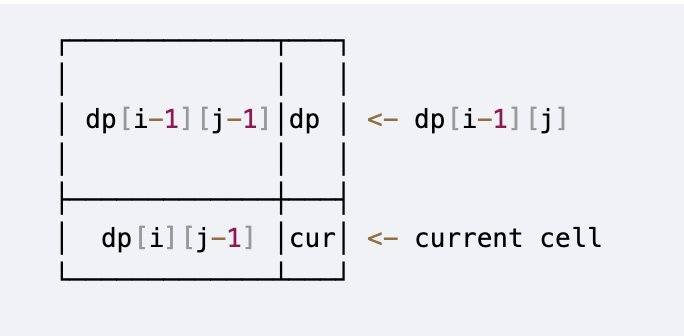
Building Intuition

Think of dp[i][j] as the “total sum of rectangle from top-left corner (0,0) to bottom-right corner (i,j)”

To calculate this sum:

  1. Add current element: grid[i][j]

  2. Add rectangle above: dp[i-1][j] (sum from (0,0) to (i-1,j))

  3. Add rectangle to left: dp[i][j-1] (sum from (0,0) to (i,j-1))

  4. Subtract overlap: dp[i-1][j-1] (counted twice in steps 2&3)

Visual representation:

Edge Cases Handling

  • Base case (0,0): dp[0][0] = grid[0][0] - just the single element

  • First row: Only add element to the left → dp[0][j] = dp[0][j-1] + grid[0][j]

  • First column: Only add element above → dp[i][0] = dp[i-1][0] + grid[i][0]

  • General case: Use full formula with overlap subtraction

Algorithm Breakdown

Step 1: 2D Prefix Sum Construction


vector<vector<int>> dp(n, vector<int>(m,0));

  • dp[i][j] = sum of all elements from (0,0) to (i,j)

  • This represents the sum of the submatrix with top-left at (0,0) and bottom-right at (i,j)

Step 2: Fill DP Array

The standard 2D prefix sum formula:


if(i==0 &amp;&amp; j==0){

dp[i][j] = grid[i][j]; // Base case

}

else if(i==0){

dp[i][j] = dp[i][j-1] + grid[i][j]; // First row

}

else if(j==0){

dp[i][j] = dp[i-1][j] + grid[i][j]; // First column

}

else {

dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + grid[i][j];

}

Why this works:

  • dp[i-1][j] = sum from (0,0) to (i-1,j)

  • dp[i][j-1] = sum from (0,0) to (i,j-1)

  • dp[i-1][j-1] = sum from (0,0) to (i-1,j-1) (counted twice, so subtract)

  • grid[i][j] = current element

Step 3: Count Valid Submatrices


if(dp[i][j] <= k) ans++;

For each position (i,j), if the sum from (0,0) to (i,j) is ≤ k, we found a valid submatrix.

Example Walkthrough

Grid = [[7,6,3], [6,6,1]], k = 18

DP Array Construction:


Position (0,0): dp[0][0] = 7

Position (0,1): dp[0][1] = 7 + 6 = 13

Position (0,2): dp[0][2] = 13 + 3 = 16

Position (1,0): dp[1][0] = 7 + 6 = 13

Position (1,1): dp[1][1] = 7 + 6 + 6 + 6 = 25

Position (1,2): dp[1][2] = 7 + 6 + 3 + 6 + 6 + 1 = 29

Valid Submatrices (sum ≤ 18):

  1. (0,0) to (0,0): sum = 7 ✓

  2. (0,0) to (0,1): sum = 13 ✓

  3. (0,0) to (0,2): sum = 16 ✓

  4. (0,0) to (1,0): sum = 13 ✓

  5. (0,0) to (1,1): sum = 25 ✗

  6. (0,0) to (1,2): sum = 29 ✗

Answer = 4

Time & Space Complexity

  • Time: O(n × m) - single pass through the grid

  • Space: O(n × m) - for the DP array

Key Takeaways

  1. Problem constraint simplification: “Contains top-left element” means all submatrices start from (0,0)

  2. 2D Prefix Sum technique: Efficiently calculate submatrix sums

  3. Single pass solution: Build prefix sums and count simultaneously

  4. Incremental building: Each dp[i][j] uses previously computed values to avoid redundant calculations

Why This Approach Works

Instead of checking all possible submatrices (which would be O(n²m²)), we leverage the constraint that all valid submatrices must start from (0,0). This reduces the problem to finding all valid bottom-right corners, which can be done in O(nm) time using prefix sums.

Graph View

Backlinks