About
Life
Daily Notes

554. Brick Wall

3 min read

Date: 11-09-2025 Time: 00:26

https://leetcode.com/problems/brick-wall/description/

Prefix Sum Approach

Core Idea: Use prefix sums to find all edge positions in each row, then find the position with the most edges across all rows.

🚀 Optimal Solution

class Solution {
public:
    int leastBricks(vector<vector<int>>& wall) {
        unordered_map<long long, int> edgeCount;  // position -> count of edges
        int n = wall.size();
        
        // For each row, calculate prefix sums to find edge positions
        for(int i = 0; i < n; i++) {
            long long prefixSum = 0;
            // Process all bricks except the last one (avoid wall boundary)
            for(int j = 0; j < wall[i].size() - 1; j++) {
                prefixSum += wall[i][j];  // Cumulative width = edge position
                edgeCount[prefixSum]++;   // Count this edge position
            }
        }
        
        // Find position with maximum edges
        int maxEdges = 0;
        for(auto& pair : edgeCount) {
            maxEdges = max(maxEdges, pair.second);
        }
        
        // Minimum crossed bricks = Total rows - Maximum edges at any position
        return n - maxEdges;
    }
};

Step-by-Step Example

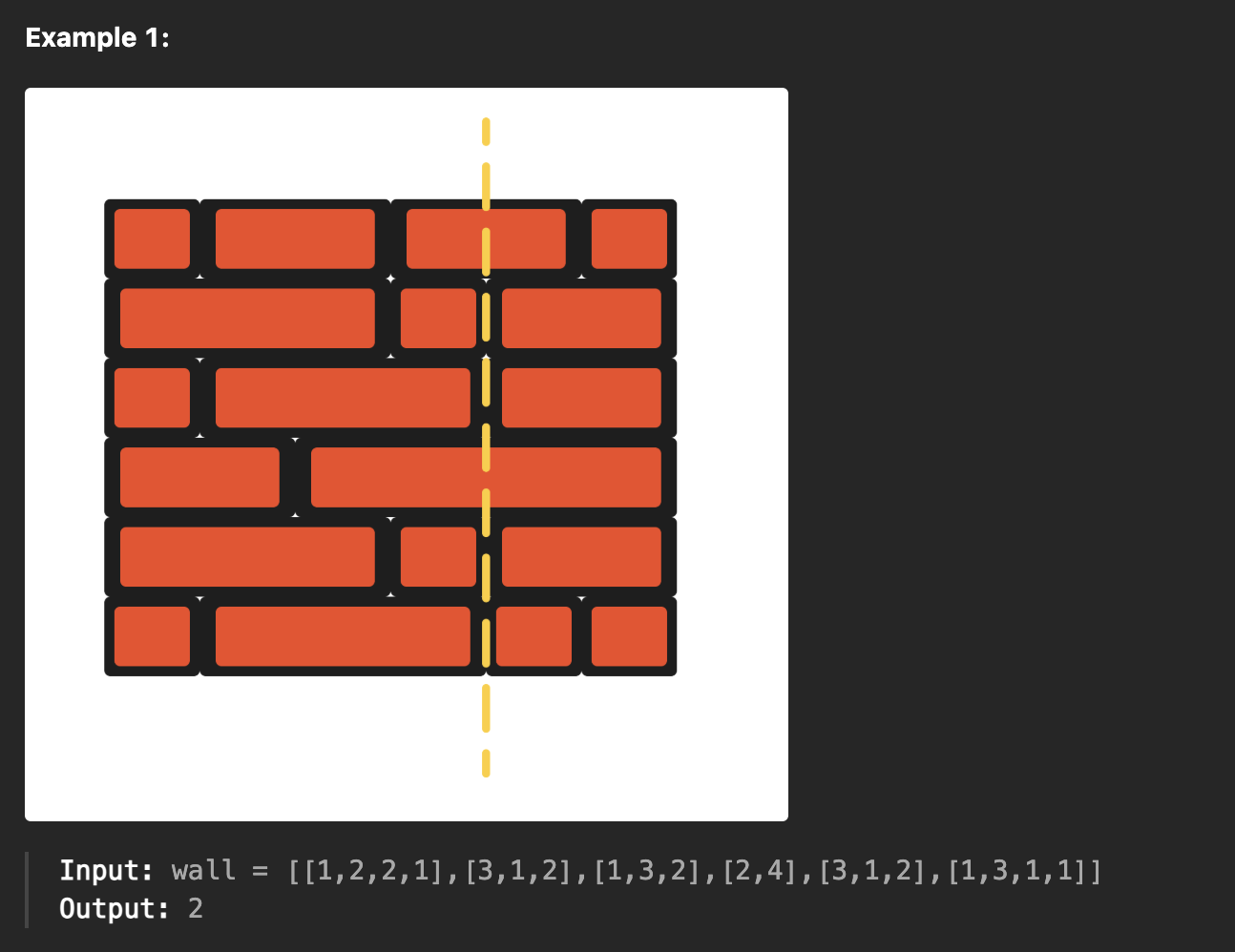
Input: wall = [[1,2,2,1],[3,1,2],[1,3,2],[2,4],[3,1,2],[1,3,1,1]]

Step 1: Calculate Prefix Sums (Edge Positions)

Row 0: [1,2,2,1]

prefixSum = 0
j=0: prefixSum = 0 + 1 = 1  → edgeCount[1]++
j=1: prefixSum = 1 + 2 = 3  → edgeCount[3]++  
j=2: prefixSum = 3 + 2 = 5  → edgeCount[5]++
// Skip last brick to avoid wall boundary
Edge positions: [1, 3, 5]

Row 1: [3,1,2]

prefixSum = 0
j=0: prefixSum = 0 + 3 = 3  → edgeCount[3]++
j=1: prefixSum = 3 + 1 = 4  → edgeCount[4]++
Edge positions: [3, 4]

Row 2: [1,3,2]

prefixSum = 0
j=0: prefixSum = 0 + 1 = 1  → edgeCount[1]++
j=1: prefixSum = 1 + 3 = 4  → edgeCount[4]++
Edge positions: [1, 4]

Row 3: [2,4]

prefixSum = 0
j=0: prefixSum = 0 + 2 = 2  → edgeCount[2]++
Edge positions: [2]

Row 4: [3,1,2]

prefixSum = 0
j=0: prefixSum = 0 + 3 = 3  → edgeCount[3]++
j=1: prefixSum = 3 + 1 = 4  → edgeCount[4]++
Edge positions: [3, 4]

Row 5: [1,3,1,1]

prefixSum = 0
j=0: prefixSum = 0 + 1 = 1  → edgeCount[1]++
j=1: prefixSum = 1 + 3 = 4  → edgeCount[4]++
j=2: prefixSum = 4 + 1 = 5  → edgeCount[5]++
Edge positions: [1, 4, 5]

Step 2: Count Edge Frequencies

edgeCount[1] = 2  (appears in rows 0, 2, 5)
edgeCount[2] = 1  (appears in row 3)
edgeCount[3] = 3  (appears in rows 0, 1, 4)  
edgeCount[4] = 4  (appears in rows 1, 2, 4, 5) ← Maximum!
edgeCount[5] = 2  (appears in rows 0, 5)

Step 3: Calculate Result

maxEdges = 4 (at position 4)
totalRows = 6
minimumCrossedBricks = 6 - 4 = 2

Why Prefix Sum Works

  1. Edge Detection: Prefix sum gives exact positions where bricks end (edges occur)
  2. Frequency Counting: Count how many rows have an edge at each position
  3. Optimal Position: Position with most edges = position that crosses fewest bricks
  4. Direct Calculation: crossedBricks = totalRows - edgesAtBestPosition

Complexity Analysis

  • Time: O(n × m) where n = rows, m = average bricks per row
  • Space: O(W) where W = total width of the wall (for storing edge positions)

Graph View